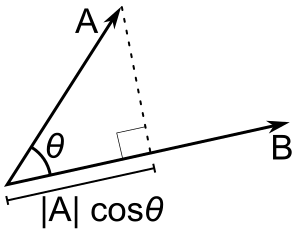
点乘
A向量 在 B向量 上的投影乘以 B向量 的长度
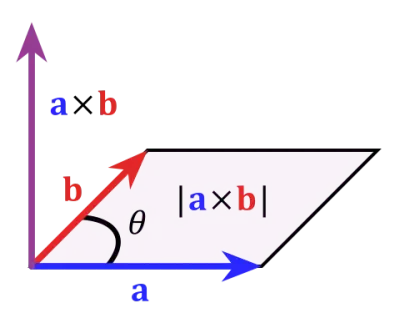
叉乘
垂直于 AB向量平面的单位向量(紫色向量)
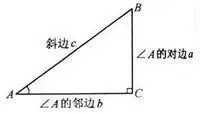
三角函数
| 函数 | 缩写 | 表达式 |
|---|---|---|
| 正弦函数 | sin | ∠A的对边比斜边 |
| 余弦函数 | cos | ∠A的邻边比斜边 |
| 正切函数 | tan | ∠A的对边比邻边 |
毕达哥拉斯定理(勾股定理)
命题:在一个直角三角形中,斜边的平方等于其他两边的平方之和
\(a^2 + b^2 = c^2\)
复数
- 虚数:i
- 虚数:\(i^2=-1\)
- 复数包含实数和虚数
- 复数:$z=a+bi$
- 复平面:水平的实轴与垂直的虚轴建立起来的复数的几何表示
模
- 复数的模
- 设复数为:\(z=a+bi\)
- 复数 z 的模:\(|z|=\sqrt{a^2+b^2}\)
- 集合意义为:复平面上一点 (a,b) 到原点的距离
- 取模运算
- 取余数
- 例:100%17=15
∑(西格玛)
求和符号 $$\sum_{i=1}^n f(i)$$ 下标 “i” 为起始值 上标 “n” 为结束值 右边 “$f(i)$” 为求和对象:为一个包含 “i” 的函数 求和过程为:将求和对象 “\(f(i)\)” 的值从起始值 “i=1” 到结束值 “i=n” 相加,得到最终的求和结果 $$\sum_{i=1}^5 i$$ 计算过程等于:1+2+3+4+5=15
幂(power)
乘方运算的结果 $2^3$ 等于 2 的 3 次幂 等于 2 的 3 次方 2 为“底数” 3 为“指数”
数
自然数(N)
0,1,2,3 …
正整数集(${N^+}$ or ${N^*}$)
1,2,3,4…
整数集(Z)
-2,-1,0,1,2…
有理数集(Q)
非无限不循环小数,如:$\pi$ 、$\sqrt{2}$
实数(R)
正数,0,复数(包含小数)
四元数
表示为:a+bi+cj+dk = w、x、y、z 其中 i、j、k 为虚数 通过四维空间描述三维旋转的方法 x、y、z 可以理解为三轴的权重 w 为 靠近圆心的比值 1 为圆形,0为球面,-1为无穷远
矩阵
左乘
表示向量坐标变换至矩阵坐标系(向量坐标改变)
$$ \begin{bmatrix} a1 & a2 & a3\\ b1 & b2 & b3\\ c1 & c2 & c3 \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix} =x \begin{bmatrix} a1\\ b1\\ c1 \end{bmatrix} +y \begin{bmatrix} a2\\ b2\\ c2 \end{bmatrix} +z \begin{bmatrix} a3\\ b3\\ c3 \end{bmatrix} = \begin{bmatrix} xa1 & ya2 & za3\\ xb1 & yb2 & zb3\\ xc1 & yc2 & zc3 \end{bmatrix} $$
右乘
表示在矩阵坐标系中向量的坐标(向量坐标不变)
$$
\begin{bmatrix}
x \\
y \\
z
\end{bmatrix}
\begin{bmatrix}
a1 & b1 & c1 \\
a2 & b2 & c2 \\
a3 & b3 & c3
\end{bmatrix} =x
\begin{bmatrix}
a1 \\
a2 \\
a3
\end{bmatrix} +y
\begin{bmatrix}
b1 \\
b2 \\
b3
\end{bmatrix} +z
\begin{bmatrix}
c1 \\
c2 \\
c3
\end{bmatrix} =
\begin{bmatrix}
xa1 + yb1 + zc1 \\
xa2 + yb2 + zc2 \\
xa3 + yb3 + zc3
\end{bmatrix}
$$
傅里叶变换
对时域的频域拆解 时域:信号的时间变化 频域:信号分解出的信号(三角函数正弦信号) 相位:起始点位置 振幅:波动的强度 低频(决定轮廓) 高频(决定细节)